Analysis I: Lecture 2

In which we think about sequences even when they don’t converge.

We proved Lemma 2.
Theorem 3 (Bolzano–Weierstrass theorem): Let $(x_n)_{n=1}^{\infty}$ be a bounded sequence of real numbers, say $|x_n| \leq K$ for all $n$ . Then there is a convergent subsequence: that is, there are $n_1 < n_2 < n_3 < \dotsb$ and a real number $x$ such that $x_{n_j} \to x$ as $j \to \infty$ . We saw one proof, using ‘zooming in’ (also known as ‘interval bisection’ and ‘lion hunting’). There was a small typo very near the end: the notes should say “ $x_{n_j} \to a$ as $j \to \infty$ ” rather than as $n \to \infty$ .

Understanding today’s lecture

Here are some exercises to get you thinking about what we discussed today.

Show that every bounded real sequence has a monotone subsequence. Deduce another proof of the Bolzano-Weierstrass theorem.
When you’ve tried the above exercise, you could try this ‘proofsorter‘ activity to consolidate your understanding of the two proofs you’ve seen.
You could try running each of the two proofs on some examples of sequences, to get a feel for what they tell us. Do they give us a way to find a convergent subsequence, or just tell us that there must be one? If they find convergent subsequences, do they find the same ones?
Is there an analogue of the Bolzano-Weierstrass theorem for sequences of complex numbers?

Preparation for Lecture 3

If a sequence converges, then eventually all the terms get really close to the limit, so they’re eventually all really close together. How could we express that idea more formally? And is the converse true? That is, if eventually all the terms get really close together, does that mean that the sequence must converge?

This entry was posted on January 21, 2013 at 1:37 pm and is filed under Cambridge Maths Tripos, IA Analysis I, Lecture. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

9 Responses to “Analysis I: Lecture 2”

apgoucher Says:
January 23, 2013 at 2:34 am
Exciting stuff. Yes, Bolzano-Weierstrass clearly generalises to R^n equipped with the Euclidean norm (and therefore in the complex numbers). We can apply Bolzano-Weierstrass to find a sequence in which the first coordinate converges and proceed inductively.

A month and a half ago (sesquimonth?), I wrote about how B-W can be used to prove König’s tree lemma and other proofs requiring compactness:

http://cp4space.wordpress.com/2012/12/05/bolzano-weierstrass/
Analysis I: Lecture 3 « Theorem of the week Says:
January 23, 2013 at 1:44 pm
[…] Expositions of interesting mathematical results « Analysis I: Lecture 2 […]
KMacfarlane Says:
January 23, 2013 at 7:57 pm
Hi, I have a question about our proof of lemma 2 (v).

We said that epsilon was small so we could assume epsilon = 1 we can find an N with |a_n b_n – ab| < epsilon?
Can we not just say something like:
|a_n| <= |a_n-a| + |a| < |a| + epsilon
and then write
|a_n b_n – ab| < |a| epsilon + epsilon^2 + |b| epsilon
= epsilon (|a| + |b| + epsilon), which is a quantity we can make arbitrarily small?

Thanks very much for reading
theoremoftheweek Says:
January 23, 2013 at 11:41 pm
Good question!

We assumed that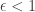 $\epsilon < 1$ (inequality rather than equality), but that might have been a typo in your comment.

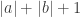This boils down to much the same thing. How do we know that we can make $\epsilon (|a| + |b| + \epsilon)$ arbitrarily small? Well, the thing in brackets is bounded (e.g. by $|a| + |b| + 1$ ) — and we're pretty much back to the proof in lectures.

Assuming that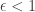 $\epsilon < 1$ doesn't cause us any difficulties. If we can show that eventually something is less than this $\epsilon$ then it'll certainly also be less than anything bigger than 1, right?

Hope that helps; post back if you have further questions.
KMacfarlane Says:
January 25, 2013 at 10:14 am
Thank you, this is much clearer now!
I did have another question about part (vi) of the same lemma, but I think I answered it myself while typing it out.
I’ll write it here in case anyone else was confused:

I wasn’t sure why
|a_n – a| |a_n| >= |a|/2,
where a_n and a are complex.

But the statement |a_n – a| < |a|/2 means that a_n lies within a circle with centre a and radius |a|/2 in the complex plane, so drawing a line from the origin to the point representing a shows that the distance from the origin to a_n must be at least the distance from the origin to the circle, which is |a|/2.
(In fact, we have a strict inequality – but the weak inequality is sufficient for what we want to prove).

I think this is what you were getting at in the lecture when you drew a picture, but I didn't see it at the time.
theoremoftheweek Says:
January 25, 2013 at 10:53 am
Thanks, it’s always good to have other people’s descriptions of how they have made sense of something.

I’m glad that typing out the question helped you to resolve it — explaining the problem to someone else is often a good strategy!
Analysis I: Lecture 8 « Theorem of the week Says:
February 4, 2013 at 12:19 pm
[…] Theorem 18: (Intermediate value theorem) Let be a function that is continuous on with . Then there is some in such that . We proved this using ‘zooming in’ or ‘interval bisection’ or ‘lion hunting’ — this was the strategy that we used in lectures to prove the Bolzano-Weierstrass theorem. […]
Arijjt Says:
August 18, 2020 at 7:55 am
Hi,

I find your post here very helpful. But your “proofsorter activity” link is broken. Can you please fix it?

Thanks!
theoremoftheweek Says:
August 18, 2020 at 8:11 am
Thanks for mentioning this, the link is now fixed.