I’ve previously written about Fermat’s Little Theorem, which tells us that if is a prime and
is not divisible by
, then
. That’s not terribly exciting when
, so let’s concentrate on odd primes
in this post. Then
is a whole number, so it makes sense (in the modular arithmetic world) to let
. Then Fermat‘s Little Theorem tells us that
.
How many possibilities for are there (modulo
, of course), if we know that
?
Well, that congruence tells us that . But, in the jargon, “there are no zero-divisors modulo a prime”. That is, if
, then
or
. (Note that we really do need
to be prime here — try some examples!)
So if is such that
, then
. Which is pretty nice. (Again, we really needed
to be prime here. Try working modulo 8 instead, and see what happens there!)
Back to where we started. We said that if is not divisible by the odd prime
, then
, so we know know that
.
That narrows down the possibilities a lot. It’s no good trying to tell me that — I simply shan’t believe you (even without doing any calculations). But tell me that
, or that
, and I have a problem — how do I know which is correct?
This is where Euler‘s criterion comes in. I think that I’ll just state it now, and then say a little about how one might prove it afterwards.
Theorem (Euler’s Criterion) Let
be an odd prime, and let
be coprime to
. Then
.
Here the symbol on the right-hand side of the congruence is the Legendre symbol.
So not only is certainly congruent to 1 or -1 modulo
, but we can tell which — it just depends whether or not
is a quadratic residue modulo
.
Looking at this another way, it gives us a way to compute the Legendre symbol (which appears slightly mysterious) — it’s just a suitable power. That can be very useful indeed.
How might we try to prove this? I’ll outline two approaches here, each using a bit of background theory.
One approach would be to make the most of the last Theorem of the Week, which tells us that there is a primitive root modulo . That is, there is some
such that each non-zero number modulo
is a power of
.
How does that help? Well, our number is coprime to
, so we must have
for some
. Now
. So we have
if and only if
divides
(using the fact that
has order
). And we can check that this happens if and only if
is even. But that’s exactly the criterion for
to be a quadratic residue, and so we’re done.
Alternatively, we could think about the polynomial modulo
. A theorem of Lagrange (an analogue of the fundamental theorem of algebra) tells us that this has at most
roots modulo
. The same applies to the polynomial
modulo
. But we have
values that satisfy one or other of these polynomials, so in fact they must each have
roots. But if
is a quadratic residue modulo
, then
for some
and so
, so the
quadratic residues modulo
must be the
roots of the polynomial
modulo
.
Why is Euler’s criterion a good thing? Partly, of course, because it’s intrinsically interesting in its own right. But also it can be applied to a bunch of number theory problems. One quick consequence, for example, is the fact that if is an odd prime then
is a quadratic residue modulo
if and only if
.
It also has relevance in the field of primality testing. We say that is an Euler pseudoprime to the base
if it `behaves like a prime’ as far as Euler’s criterion is concerned: if
. It turns out that if
is an odd composite number then
is an Euler pseudoprime to at most half of all possible bases, and this gives rise to the Solovay-Strassen primality test. This is very different from the situation for Fermat pseudoprimes, where there are Carmichael numbers (numbers that cannot be distinguished from primes just using this notion of a pseudoprime).
Further reading
This is another result that occurs in introductory number theory books such as The Higher Arithmetic by Davenport, and A concise introduction to the theory of numbers by Baker (to name but two examples).
February 4, 2012 at 9:33 pm
[…] 20 (Euler‘s criterion): Let be an odd prime, and let be an integer. Then . This is interesting only when is […]
February 6, 2012 at 9:43 am
I always liked the following proof of Euler’s Criterion, as it is very much like the standard proof of Wilson’s Theorem, so it’s easy to remember and recreate. Say that and
and  are “associates” if
are “associates” if  . Clearly each
. Clearly each  has a unique associate, and there are two self-associate elements if
has a unique associate, and there are two self-associate elements if  is a quadratic residue (assuming
is a quadratic residue (assuming 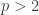 ), and none otherwise.
), and none otherwise.
We multiply out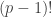 , which is congruent to
, which is congruent to 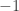 by Wilson’s Theorem. If
by Wilson’s Theorem. If  is not a quadratic residue then in the product we get all
is not a quadratic residue then in the product we get all 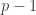 numbers pairing up with their associates, that is
numbers pairing up with their associates, that is  copies of
copies of  , and so
, and so  .
.
On the other hand, if is a quadratic residue, say with
is a quadratic residue, say with  , then in the product we get
, then in the product we get 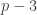 numbers pairing up with their associates, along with
numbers pairing up with their associates, along with  not pairing up. So the product is
not pairing up. So the product is  , and so
, and so  .
.
February 26, 2012 at 3:53 pm
Reblogged this on Guzman's Mathematics Weblog and commented:
https://theoremoftheweek.wordpress.com
July 31, 2012 at 10:41 am
[…] going to write this post on the assumption that you know about Fermat’s little theorem and Euler’s criterion. Fortunately, those links take you to places on this blog where you can read everything you need […]
October 23, 2013 at 10:51 am
[…] Theorem 20 (Euler’s criterion): Let be an odd prime, and let be an integer. Then . We proved this by first showing that and then using Lagrange’s theorem to show that the even powers of a primitive root ‘use up’ all the possible solutions to . […]
October 25, 2013 at 10:50 am
[…] Proposition 23 (Gauss‘s Lemma): Let be an odd prime, and let be coprime to . Then , where . We proved this by showing that , , …, correspond to , , …, in some order, where each of these has a definite sign, and then multiplying them all together to show that . Then we finished off using Euler’s criterion. […]